Thangavel PrasanthTP

Functions

2 min read

Linear function

A function is strictly linear if it satisfies two properties:

  1. Homogeneity: f(cx) = cf(x) (scaling the input scales the output by the same factor).
  2. Additivity: f(x + y) = f(x) + f(y) (the function of a sum is the sum of the functions).

A crucial consequence of these properties is that a linear function must pass through the origin. If you plug in x=0, you will always get f(0)=0. The general form of a linear function of one variable is f(x) = mx

Affine function

An affine function is a linear function followed by a translation. It doesn’t have to pass through the origin. The general form of an affine function of one variable is f(x) = mx + c, where ‘c’ is the translation constant (the y-intercept). If c is zero, the affine function is also a linear function.

An affine function is a mathematical expression formed by a linear transformation and a translation (or shift). In its simplest form, for a function from one real number to another, it can be expressed as f(x) = mx + b, where m is the slope and b is the y-intercept. Affine functions preserve collinearity and parallelism, meaning straight lines remain straight lines and parallel lines remain parallel after an affine transformation.

1

All linear functions are affine functions, but not all affine functions are linear

In many high school math classes, anything that graphs as a straight line is called a linear function. However, in more advanced mathematics, like linear algebra, the definitions become stricter.

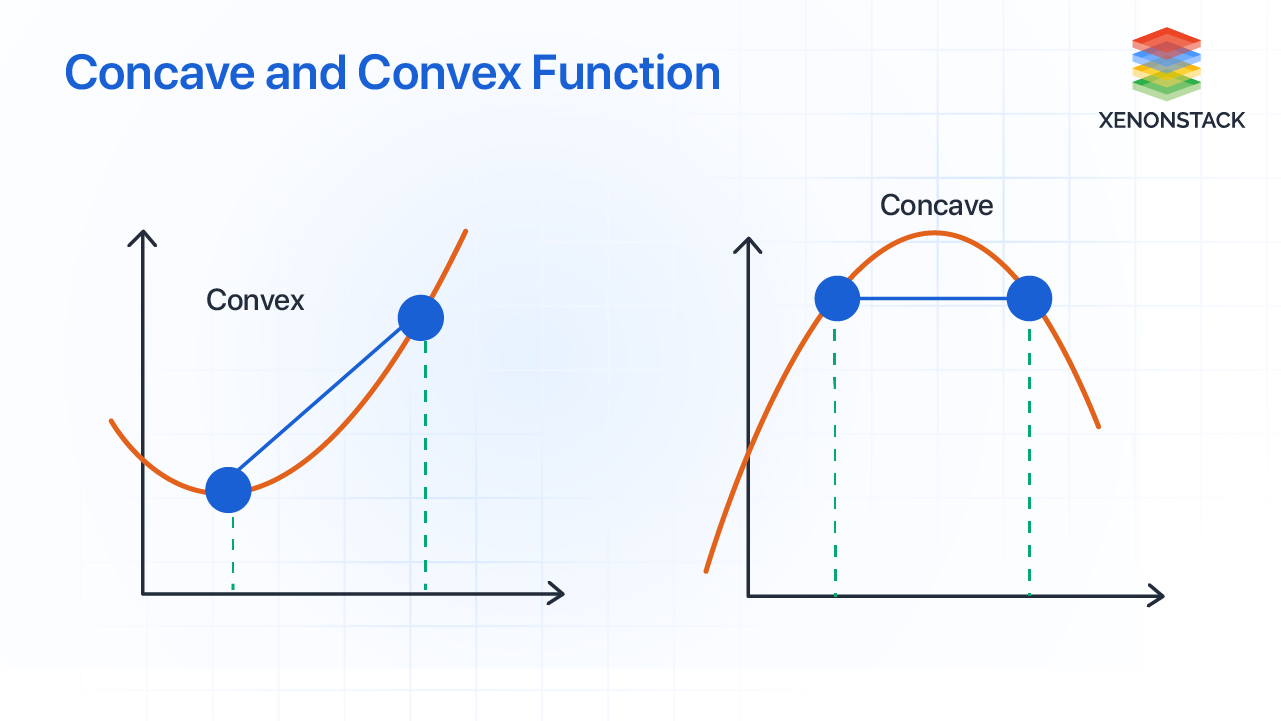
Convex and concave function

2

A straight line (so, linear and affine functions) is both concave and convex function. 1

For more details, refer concave-convex.ipynb

Concave function

…

Convex function

…

3 key properties of convex function:

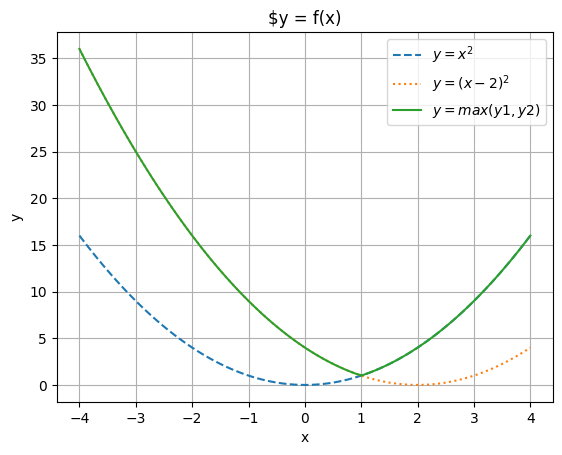
Property 1: The Pointwise Maximum of Convex Functions is Convex.

i.e., If you have a collection of convex functions , then the new function is also convex.

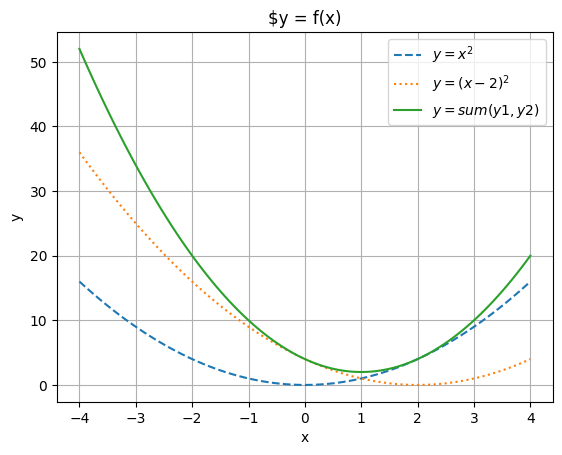
Property 2. The Sum of Convex Functions is Convex.

i.e., If and are convex functions, then their sum is also convex. This extends to any finite sum of convex functions.

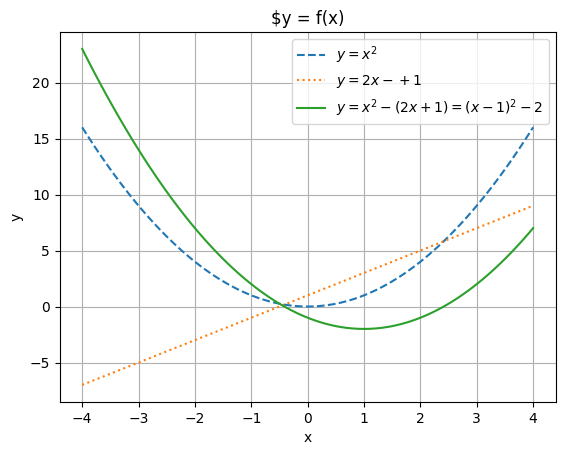
Property 3: Subtracting an Affine Function from a Convex Function Preserves Convexity.

Footnotes

  1. https://www.google.com/url?sa=i&url=https%3A%2F%2Fmath.stackexchange.com%2Fquestions%2F3361379%2Faffine-and-linear-functions&psig=AOvVaw2gytlwDDkWdFGVaWBLoz-6&ust=1755945282428000&source=images&cd=vfe&opi=89978449&ved=0CBkQ3YkBahgKEwjItJyInJ6PAxUAAAAAHQAAAAAQgwE ↩

  2. https://www.xenonstack.com/glossary/concave-and-convex-function ↩

Graph View

Backlinks