Skew

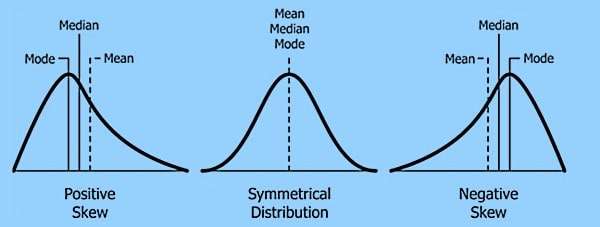
Skewness measures the asymmetry of a data distribution, indicating if data points are clustered more on one side of the mean, creating a longer "tail" in that direction.

Type of Skewness

Skew Type	Skew Type	Mean vs. Median vs. Mode	Description
Symmetrical	Zero Skew	$\text{mean}=\text{median}=\text{mode}$
Left Skewed	Negative Skew	$\text{mean}<\text{median}<\text{mode}$	Longer tail to the left; few small values
Right Skewed	Positive Skew	$\text{mean}>\text{median}>\text{mode}$	Longer tail to the right; few large values

• Zero Skew (Symmetrical): The data is evenly distributed; the mean, median, and mode are close or equal (like a bell curve).
• Positive Skew (Right Skewed): The tail extends to the right; most data points are smaller, with a few large values. The mean is greater than the median.
• Negative Skew (Left Skewed): The tail extends to the left; most data points are larger, with a few small values. The mean is less than the median.

Transclude of left-or-right-skewed-1.avif

Transclude of left-or-right-skewed-2.avif

Source: Skewed Distributions may not be normal, but they don’t have to be complicated!