Embeddings

Definition

Embedding - The concept of converting text (or other data) into a numerical vector representations, a format that NNs can understand and process.

An "embedding" is a low-dimensional vector representation of a higher-dimensional object (like a geohash, a specific time slot, english words, or the learned behavior from a complex model). The idea is that similar objects will have similar embeddings.

 

Why should we represent text using vectors?

For a computer to understand human-readable text, we need to convert our text into a machine-readable (i.e., numerical) format.

Language is inherently full of information, so we need a reasonably large amount of data to represent even small amounts of text. Vectors are naturally good candidates for this format.

We also have two options for vector representation; sparse vectors or dense vectors.

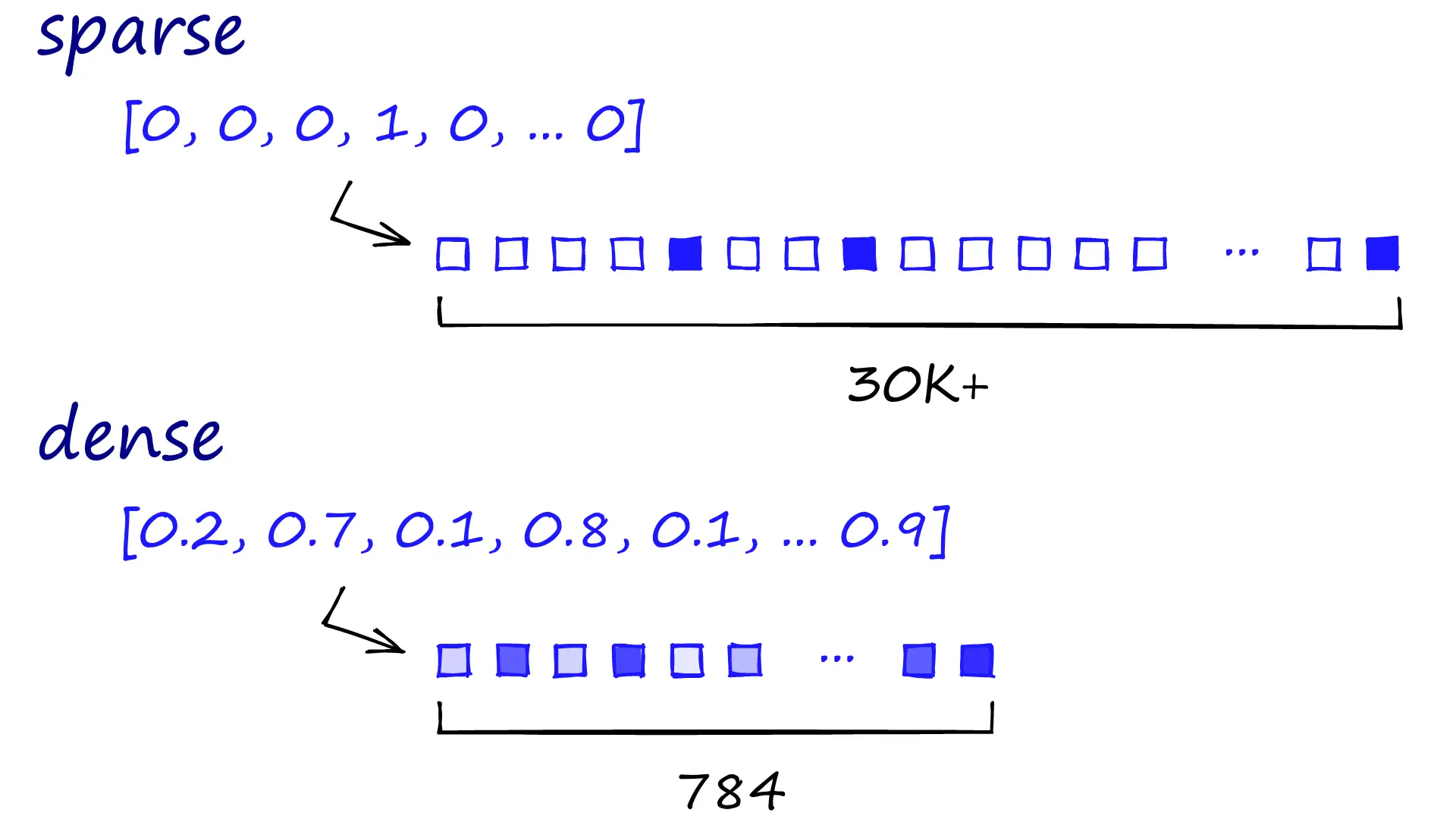
Sparse vs. Dense embeddings

We also have two options for vector representation; sparse vectors or dense vectors.

Sparse vectors are high-dimensional and primarily composed of zeros, with each non-zero dimension often representing a specific, explicit feature like a word’s presence, while dense vectors are lower-dimensional (when compared to sparse vectors) and have mostly non-zero values, capturing contextual and semantic meaning through learned, abstract relationships between features. Typically, we are taking words and encoding them into very dense, high-dimensional vectors. The abstract meaning and relationship of words are numerically encoded. ¹

Sparse vectors are called sparse because vectors are sparsely populated with information. Typically we would be looking at thousands of zeros to find a few ones (our relevant information). Consequently, these vectors can contain many dimensions, often in the tens of thousands.

Dense vectors are still highly dimensional (784-dimensions are common, but it can be more or less). However, each dimension contains relevant information, determined by a neural net — compressing these vectors is more complex, so they typically use more memory.

Syntax vs. Semantics

• Sparse vectors: numerical representations of text syntax
• Dense vectors: numerical representations of text semantic meaning

¹

Why (Benefits of Embeddings)?

• Capturing Semantic Relationships: Embeddings learn a dense vector representation for each category (e.g., taxi type IDs, geohashes, time contexts). In this vector space, categories with similar meanings or properties will be closer to each other. This allows the model to understand and leverage the underlying relationships between different categories, even if these relationships are not explicitly defined in the raw input. For example, “Premium” and “Standard” taxi types might have closer embeddings than “Premium” and “Bike” if they share more operational characteristics or user behavior patterns.
• Efficiency for Large Category Spaces: When dealing with categorical features that have many unique values (e.g., thousands of geohashes or many different taxi type IDs), one-hot encoding creates a very wide and sparse input vector. This can lead to:
  • High Dimensionality: A large number of input features, increasing model complexity and training time.
  • Sparsity: Most values in the one-hot encoded vector are zero, which can make it harder for models to learn meaningful patterns and require more data.
  • Lack of Generalization: One-hot encoding treats each category as completely independent, so the model cannot generalize well to unseen categories or leverage similarities between existing ones.

How (Embeddings achieve these benefits)?

• Learning Representations: Embeddings are typically learned during the model training process (e.g., as part of a neural network). An embedding layer maps each categorical ID to a dense vector of a predefined size (e.g., 8, 16, 32 dimensions). These vectors are initialized randomly and then adjusted via backpropagation as the model learns to minimize its loss function.
• Dimensionality Reduction: Instead of a sparse vector with potentially thousands of dimensions (for one-hot encoding), an embedding reduces the representation to a much smaller, dense vector. This makes the input more compact and efficient for the neural network to process.
• Semantic Closeness: The learning process encourages categories that frequently co-occur or have similar impacts on the prediction task to have similar embedding vectors. This effectively "encodes" the semantic relationships into the numerical space.
• Example in Uber context: For “taxi type ids”, embeddings for different taxi types would allow the model to understand which types are similar (e.g., premium variants) and which are distinct (e.g., 2-wheelers vs. 4-wheelers), even if the model hasn’t seen every single permutation of these types in specific scenarios. Similarly, for “GH & Time embeddings”, embeddings can capture that certain geohashes have similar supply-demand patterns or user behaviors during specific time slots.

Different type of embeddings

Type of Embedding	Definition	Purpose	Example
Word Embeddings	Represent individual words as dense vector.	Capture semantic & synatic relationship between words.	Word2Vec, GloVe, FastText, ELMo, BERT
Subword/Character Embeddings	Represent subword units or characters	Handle rar or out-of-vocabulary words by breaking them into small units.	Byte Pair Encoding (BPE), SentencePiece, FastText
Sentence Embeddings	Represent entire sentence as a single vector	Capture the overall meaning or intent of a sentence	InferSent, Universal Sentence Encoder, SBERT
Paragrah Embeddings	Represent a paragraph as a single vector, aggregating sentences	Summarize a collection of sentences in a coherent representation.	Doc2Vec(Paragraph Vector)
Document Embeddings	Represent an entire document or text as a single vector	Enable document-level tasks like clustering, classification, and retrieval.	Doc2Vec, Longformer, BigBird
Contextualized Token Embeddings	Represent tokens in a sequence, influenced by their context	Essential for tasks where token meaning depend on the surrounding context (e.g, NER)	Outputs from BERT, GPT, RoBERTa
Multi-modal Embeddings	Combine text with other modalities like images or audio.	Enable tasks like image captioning, video description, or cross-modal retrieval	CLIP, ALIGN
Knowledge Graph Embeddings	Represent entities and relationships in a knowledge graph.	Enable reasoning over structured data like knowledge graphs.	TransE, TransR, Node2Vec, DeepWalk
Cross-lingual/Multilingual Embeddings	Align semantic meaning across multiple languages.	Useful for translation and multilingual NLP.	mBERT, XLM-R
Task-Specific Embeddings	Embeddings tailored for specific NLP tasks or domains.	Fine-tuned to optimize for specific tasks (e.g., sentiment analysis, question answering).	Fine-tuned BERT, GPT, BioBERT, SciBERT

Word embeddings vs. Contextualised token embeddings

Summary

• Word Embeddings are simpler and static, making them fast and lightweight but limited in handling word ambiguity.
• Contextualized Token Embeddings are dynamic and context-aware, making them powerful for nuanced tasks but computationally intensive.

The key difference between word embeddings (like Word2Vec or GloVe) and contextualized token embeddings (like those produced by BERT) lies in how they handle context and the resulting representation of words or tokens.

1. Context Awareness

Aspect	Word Embedding	Contextualized Token Embedding
Context Sensitivity	Static: Same embedding for a word regardless of context.	Dynamic: Embeddings depend on the surrounding context.
Example	”bank” has the same embedding in “river bank” and “bank account”.	“bank” in “river bank” has different embedding than “bank account”.

2. Representation Type

Aspect	Word Embedding	Contextualized Token Embedding
Representation	A single fixed vector for each word in the vocabulary.	A unique vector for each occurrence of a token, with varying context.
Granularity	Focused on capturing global relationships between words.	Captures both global and local (context-dependant) relationships.

3. Model and Architecture

Aspect	Word Embedding	Contextual Token Embedding
Underlying Model	Simple architecture like shallow neural network.	Deep architectures like transformers (e.g, BERT, GPT).
Training Method	Trained to predict nearby words or co-occurrence.	Pre-trained on massive corpora with tasks like masked language modelling (MLM), or predicting the next word.

4. Flexibility and Use Cases

Aspect	Word Embedding	Contextual Token Embedding
Vocabulary Size	Requires a predefined vocabulary, struggles with OOV words.	Handles OOV words with subword tokenization (e.g., WordPiece, BPE)
Suitability	Good for simpler tasks where context isn’t crucial (e.g., word similarity)	Essential for tasks requiring deep understanding of the context (e.g., NER, question answering)

5. Computational Complexity

Aspect	Word Embedding	Contextual Token Embedding
Efficiency	Lightweight and computationally efficient	Computationally expensive due to the deep transformer architecture
Inference Speed	Faster as embeddings are precomputed and static.	Slower as embeddings are generated dynamically for each input

Embeddings Size

Refer GPT comparison for embedding size of different GPT models.

• For e.g., GPT-1 and GPT-2 Small (both 117M parameters) use an embedding size of 768 dimensions, where as GPT-3 Davinci (175B parameters) use an embedding size of 12,288 dimensions (16x of the former).

Embedding vectors using models/text-embedding-004 from Google gemini

Source: [[Google-5-Day-Gen-AI-Intensive-Course#[Day 2 - Embeddings and similarity scores [TP (https //www.kaggle.com/code/prasanth07/day-2-embeddings-and-similarity-scores-tp)|Google5-Day-Gen-AI-Intensive-Course > Embeddings]]

The text highlighted explains how to measure the similarity between the embedding vectors generated by the embed_content function.

Here’s a breakdown:

1. Embedding Vectors: When we use a model like models/text-embedding-004 from Google gemini, it converts text (like our sentences) into numerical representations called embedding vectors. These vectors capture the semantic meaning of the text.

Texts with similar meanings will have embedding vectors that are "closer" to each other in the vector space.

2. Inner Product (${\mathbf{u}}^T\mathbf{v}$): The inner product (also known as the dot product) is a mathematical operation that takes two vectors and returns a single number. For embedding vectors, the inner product is used as a measure of similarity.

A higher inner product generally indicates higher similarity between the two texts that the vectors represent.

3. Normalized Vectors and Cosine Similarity: The text mentions that the API provides embedding vectors that are normalized to unit length. This means each vector has a length (or magnitude) of 1. When vectors are normalized, their inner product is mathematically equivalent to the cosine similarity between them. Cosine similarity measures the cosine of the angle between two vectors. If the vectors point in the same direction (angle is 0 degrees), the cosine is 1, indicating high similarity. If they are perpendicular (angle is 90 degrees), the cosine is 0, indicating no similarity. If they point in opposite directions (angle is 180 degrees), the cosine is -1, indicating high dissimilarity. Since these vectors are normalized, the inner product will range from -1 to 1.

However, in the context of semantic similarity with this type of embedding, the scores typically range from 0.0 (completely dissimilar) to 1.0 (completely similar) as mentioned in the heatmap description.

4. Matrix Self-Multiplication (df @ df.T): If our embedding vectors are stored in a matrix or DataFrame df, where each row is an embedding vector for a piece of text, the operation df @ df.T performs matrix multiplication of the DataFrame by its transpose. This creates a similarity matrix showing the pairwise similarity between all texts in our list.
5. Heatmap Visualization: The resulting similarity matrix can be visualized as a heatmap. As the text describes, a range from 0.0 (completely dissimilar) to 1.0 (completely similar) is depicted from light (0.0) to dark (1.0). This allows you to quickly see which texts in your list are most similar to each other based on their embedding vectors.

Footnotes

1. https://www.pinecone.io/learn/series/nlp/dense-vector-embeddings-nlp/ ↩ ↩²